Jean-Baptiste Excoffier - Data scientist

L’analyse automatique d’images a vu ses performances grandement améliorées ces dernières années.

Cela provient principalement de l’augmentation des capacités de calculs des ordinateurs ainsi qu’à l’évolution des modèles d’apprentissage profond (Deep Learning) basés sur des réseaux neuronaux, dont nous avons décrit les évolutions dans l’article précédent. Ces techniques sont aujourd’hui régulièrement appliquées à l’imagerie médicale, notamment pour le dépistage, comme la détection précoce de maladies oculaires par exemple.

Toutefois ces modèles, bien que performants, soulèvent aussi la problématique de la confiance que les utilisateurs (ingénieurs, médecins, décideurs) ainsi que les personnes impactées (patients notamment) peuvent réellement leur accorder [1]. En effet, lors de son apprentissage un modèle peut se baser sur des éléments qui ne sont pas considérés comme réellement pertinents par les experts du domaine. Par exemple, un modèle construit sur des images radiologiques pour de la détection de maladies pulmonaires se basait régulièrement sur un sigle situé en haut à droite de l’image pour effectuer sa prédiction, alors même que celui-ci n’était en aucun cas une information clinique [2]. Le modèle avait en effet détecté que la répartition des sigles n’était pas homogène parmi les maladies, donc utilisait cette information.

Par conséquent il est crucial de mieux comprendre le pourquoi de la décision d’un modèle, afin d’éviter ces effets souvent surnommés effets Hans le malin [3] indiquant que le modèle s’est entre autres appuyé sur des artefacts

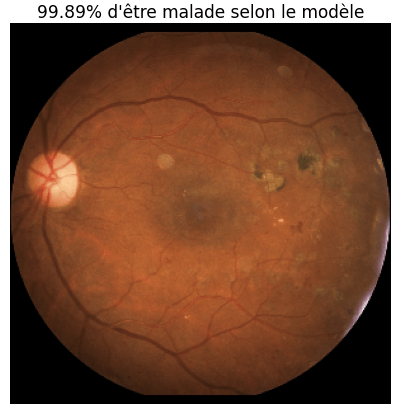
La figure 1 représente un exemple de prédiction effectuée par un modèle de réseau neuronal dans un objectif de détection de patients atteints de rétinopathie diabétique, qui est une maladie oculaire résultant d’une complication du diabète [4]. Le modèle s’est donc en premier lieu entraîné, sur des images d’un jeu de données open source [5] provenant d’examens de fond d’œil, à distinguer les patients sains des malades [6].

Ensuite, l’image de la figure 1, qui est celle d’un patient malade lui est proposée, et le modèle effectue une prédiction. Nous remarquons que la prédiction est correcte, puisque la probabilité que l’image appartienne à un patient malade estimée par le modèle est très élevée. Or, nous souhaiterions savoir sur quelles parties de l’images s’est appuyé le modèle pour effectuer cette prédiction, donc trouver les zones les plus importantes dans sa décision.

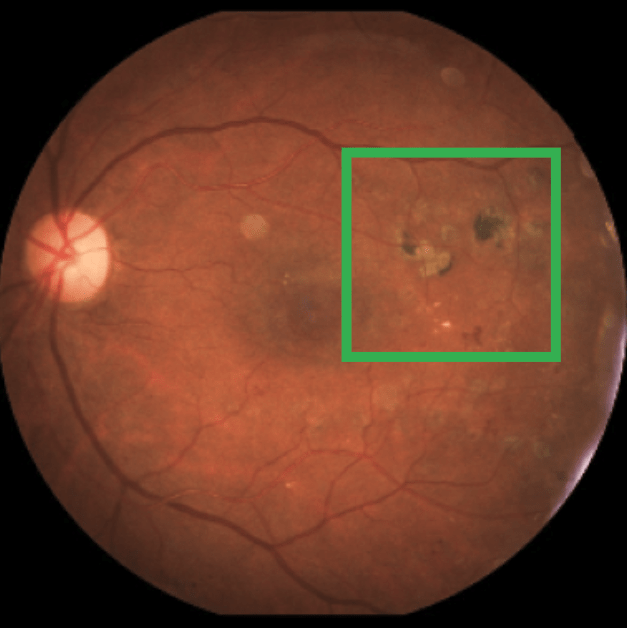
En effet, une zone ressort comme étant a priori une indication de l’état du patient, c’est la zone encadrée en vert, Figure 2, qui entoure une lésion micro vasculaire. Bien noter que pendant son entraînement le modèle n’a pas spécifiquement appris à détecter de telles zones, mais a seulement pu se baser sur l’image originale ainsi que sa classe réelle. Néanmoins, il est souhaitable que le modèle s’appuie entre autres sur cette lésion (zone verte) et non pas sur un potentiel artefact. Ainsi, de multiples méthodes ont été développées afin de mieux comprendre la prédiction d’un modèle neuronal.

Ces techniques que nous allons présenter appartiennent au domaine de l’explicabilité, souvent abrégé en XAI pour eXplainable Artificial Intelligence, et permettent de visualiser les zones les plus importantes dans la prédiction du modèle [7, 8].

Visualisation des convolutions

Une fois le réseau neuronal entraîné et ses coefficients fixés, un moyen de mieux comprendre la décision du modèle est de regarder en détails ses différents filtres convolutifs. Ce sont en effet ces couches qui manipulent le plus l’image, notamment en intégrant l’intensité de ses pixels ainsi que leur proximité spatiale.

Néanmoins, un réseau de neurones se compose généralement d’un nombre élevé de filtres convolutifs, au minimum une dizaine pour des modèles plutôt anciens jusqu’à une bonne centaine pour les actuels, empêchant de tous les analyser en détails.

Ainsi, une première approche a été publiée dans l’article [9] en 2016 prenant en compte la dernière couche convolutive d’un réseau. Nommée Class Activation Map (abrégée en CAM), cette méthode se base sur les sorties, qui varie selon l’image utilisée, de cette couche convolutive pour estimer les zones importantes de la convolution vis à vis de l’image. Etant donné que la taille de la dernière couche convolutive est très inférieure à celle de l’image originale, il nous faut ensuite redimensionner le résultat de la CAM pour correctement visualiser les zones considérées par cette technique comme étant importantes dans la prédiction fournie par le modèle.

Néanmoins, cette méthode CAM a l’inconvénient de ne pouvoir se baser que sur une architecture bien particulière (une convolution suivie d’une couche de Global Average Pooling) empêchant de fait son utilisation dans de nombreux cas. Ainsi, la méthode appelée GradCAM, publiée en 2017 dans l’article [10], se base sur CAM mais sans restriction d’architecture, mis à la part la nécessité de regarder une couche convolutive. GradCAM utilise de plus les gradients, d’où son nom, des couches pour estimer l’impact de chaque zone.

De plus, cette méthode permet de voir l’impact de couches convolutives à différents niveaux du réseau neuronal, et non plus seulement la dernière. Il est alors possible de suivre l’évolution du traitement de l’image dans le modèle. La figure 3 montre les résultats fournis par la méthode GradCAM++, une amélioration de la GradCAM publiée en 2018 [11], pour trois couches convolutives. Les résultats sont redimensionnés à la taille de l’image originale puis superposés à cette dernière.

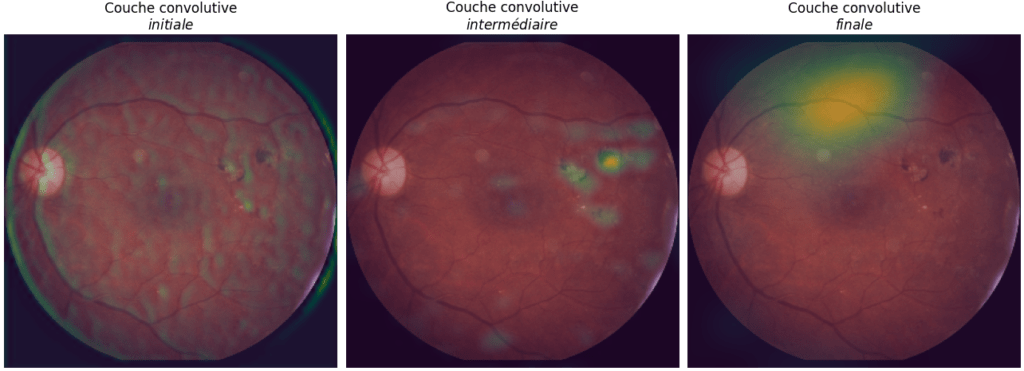
Le résultat à gauche (initiale) provient d’une couche convolutive située dès l’entrée du réseau neuronal. Nous remarquons qu’aucune zone ne se détache, l’image semblant plutôt manipulée dans son ensemble.

Le résultat du centre (intermédiaire) est issu d’une couche convolutive située plus ou moins à mi-parcours du modèle. Cette fois, la convolution semble privilégier une zone restreinte de l’image, qui est celle identifiée comme étant une lésion oculaire, donc un signe plutôt clair de maladie. Le dernier résultat, à droite (finale), provient de la dernière couche convolutive. Encore une fois une zone se détache, mais ce n’est plus la même que précédemment.

Ainsi, les méthodes de Class Activation Map donnent un meilleur aperçu du parcours de l’image dans le modèle, donc de son processus de décision. Néanmoins, comme nous avons pu le constater dans la figure 3, les résultats peuvent être sensiblement différents selon le niveau auquel nous nous plaçons. Il serait par conséquent intéressant de disposer d’une méthode plus globale, afin de bien prendre en compte en une visualisation les impacts apportés par chaque couche du réseau.

Carte de saillance

Les méthodes dites de cartes de saillance (Saliency Mapsen en Anglais) ont pour but de regarder l’impact de chaque pixel sur la prédiction du modèle, fournissant ainsi une explication générale de la décision.

Une première version est publiée en 2013 dans l’article [12]. Nommée Vanilla Gradient, cette méthode calcule l’impact des pixels en approximant leur gradient respectif sur la prédiction.

Cette technique peut être améliorée en utilisant plusieurs versions de l’image originale légèrement perturbées, via l’ajout de bruit Gaussien. Ces différents résultats sont ensuite moyennés pour former la visualisation finale. Cette amélioration, nommée SmoothGrad et publiée en 2017 dans l’article [13], permet de mieux prendre en compte les différentes parties de l’images, la carte de saillance produite par la technique de Vanilla Gradient se focalisant souvent uniquement sur une seule zone.

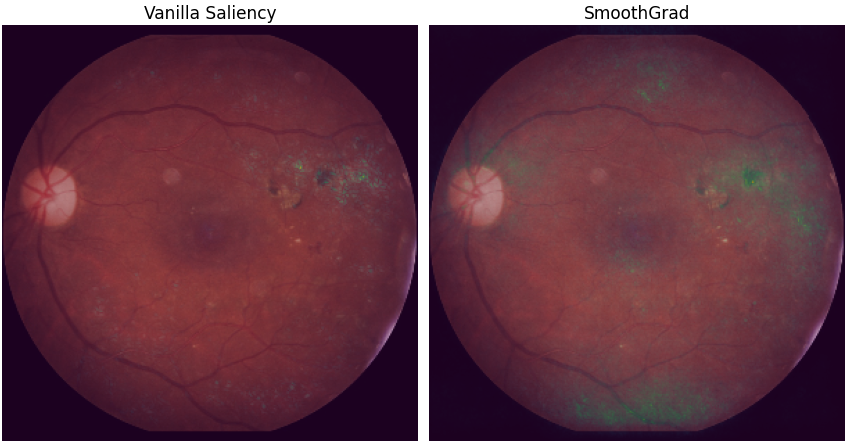
La figure 4 montre pour notre image les résultats des deux techniques de carte de saillance présentées ci-dessus. La méthode Vanilla Gradient fait principalement ressortir la zone identifiée a priori comme un signe clinique de la maladie, tandis que son amélioration en utilisant l’algorithme SmoothGrad indique trois zones supplémentaires : une située en haut de l’image (comme c’était le cas pour le résultat de la GradCAM ++ pour la dernière couche convolutive), une zone légèrement au-dessus de la fovéa, et la partie basse de l’image. Néanmoins, la zone la plus importante et scintillante est toujours la lésion située à droite de l’image, indiquant une bonne cohérence entre les méthodes.

Bien que ces différentes techniques de visualisations permettent une meilleure compréhension du modèle, elles restent spécifiques aux réseaux neuronaux. Par conséquent, il serait aussi avantageux d’avoir une méthode applicable à tout type de modèle.

LIME

Une méthode d’explicabilité est dite agnostique lorsqu’elle peut s’appliquer à tout modèle. C’est le cas de la technique Local Interpretable Modelagnostic Explanations, abrégée en LIME, publiée en 2016 dans l’article [14], qui s’appuie sur des perturbations de l’image pour identifier les zones impactant le plus la prédiction.

Une méthode d’explicabilité est dite agnostique lorsqu’elle peut s’appliquer à tout modèle.

La première étape est de segmenter l’image dont nous souhaitons expliquer la décision. La figure 5 montre un exemple de segmentation, les différentes zones étant souvent appelées des superpixels, avec la méthode dite Quickshift.

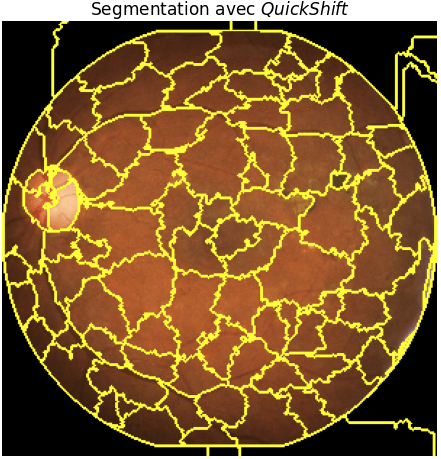
Plusieurs algorithmes de segmentation sont disponibles [15], néanmoins l’objectif n’est pas d’effectuer la segmentation la plus précise et fine possible, mais plus simplement de découper l’image pour ne pas avoir à gérer un trop grand nombre de zones. En effet, la méthode LIME va perturber l’image en occultant certaines zones (une seule ou plusieurs zones en même temps) issues de la segmentation (en les remplissant d’une seule couleur, noire par exemple) puis voir ce que prédit le modèle pour l’image modifiée. Ainsi, plus la segmentation est fine, plus le nombre de perturbations possible est élevé, rendant la méthode très lente. Par conséquent, ce n’est pas la peine en pratique d’effectuer une segmentation très poussée.

La figure 6 montre différentes perturbations et les prédictions respectives données par le modèle. L’image originale est à gauche, la prédiction fournie par le modèle étant que le patient a une probabilité de 99.89% d’être malade. Au centre, la perturbation concerne les superpixels situés au niveau de la lésion oculaire. Or nous voyons que la prédiction fournie pour cette perturbation de l’image est nettement plus basse que l’originale (72%).Pour l’image de droite, la prédiction ne change quasiment pas comparée à l’originale (95%), alors que la zone occultée est plus étendue que pour la perturbation précédente, indiquant que la zone centrale de l’image n’est pas vraiment décisive dans la prédiction du modèle.

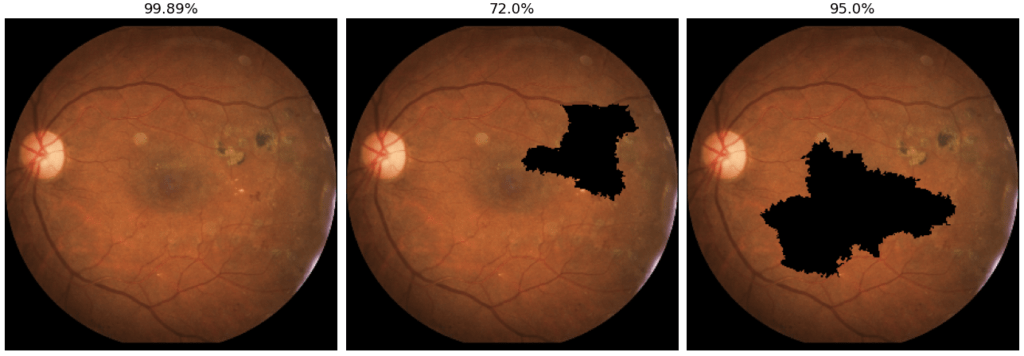
La méthode LIME répète de nombreuse fois ce processus de perturbation-prédiction, puis pondère chaque perturbation en fonction de sa similarité avec l’image originale, une image peu perturbée ayant un poids plus important. Par exemple, l’image du milieu de la figure 6 aura plus de poids que celle de gauche, puisqu’elle a une plus petite zone occultée que cette dernière. Enfin, les zones impactant le plus la prédiction sont détectées en identifiant les perturbations (et leurs superpixels occultés associés) ayant le plus d’écart avec la prédiction originale. Ainsi, les superpixels sur le signe clinique sont considérés comme plus impactant que les superpixels centraux, puisque la perturbation du milieu (figure 6) a une prédiction de 72%, ce qui, comparé à la perturbation des superpixels centraux (95%), est plus éloigné de la prédiction originale (99.89%).

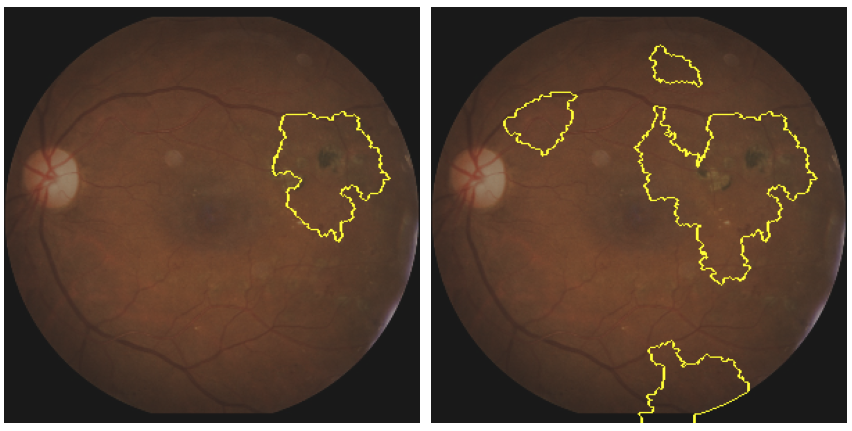
La figure 7 présente les résultats fournis par la méthode LIME appliquée à notre image.

Nous pouvons définir un seuil pour ne retenir que les zones (ie. superpixels) les plus fortement impactantes(image de gauche), mais aussi relâcher un peu ce seuil pour identifier d’autres zones influençant la prédiction, mais sans l’être autant que les premières (image de droite).

Nous voyons ainsi encore une fois que la zone clairement détectée comme étant la plus importante est celle de la lésion microvasculaire. Mais aussi que d’autres parties de l’image (en bas et proche de la fovéa) sont aussi relativement importantes. Cela correspond bien aux résultats de la carte de saillance, reflétant une forte cohérence entre ces méthodes.

Conclusion

Avec la nette amélioration des performances des modèles d’analyse automatique d’image, notamment dans l’objectif de classification, de nombreuses méthodes ont été développées afin d’avoir une meilleure compréhension des décisions de ces modèles. Ainsi il est possible de détecter si ces derniers ne s’appuient pas sur des artefacts, mais bien sur des éléments pertinents (signes cliniques par exemple) pour effectuer leurs prédictions.

Certains points restent toutefois à améliorer. Ces techniques fonctionnent notamment très bien lorsque les signes sont dans une zone restreinte. Cependant, elles sont moins efficaces lorsque le modèle se base sur des motifs plus généraux de l’image. Or, cela est souvent le cas en imagerie médicale. Par exemple, la rétinopathie diabétique est souvent détectée en se basant sur la densité et la tortuosité des vaisseaux sanguins rétiniens [16], qui sont des mesures générales. Par conséquent les techniques de visualisations actuelles ont plutôt du mal à bien faire apparaître que le modèle s’est bien basé, entre autres, sur ce type de caractéristiques pour effectuer sa prédiction.

Ces récentes avancées ont néanmoins grandement amélioré la construction de modèles prédictifs en imagerie, en augmentant leur fiabilité et la confiance qu’il est possible de leur accorder, que ce soit en termes de performances pures (précision) mais aussi de cohérences avec les connaissances des experts du domaine d’application.

Découvrir notre projet de recherche dédié à l'explicabilité de modèles et de résultats de prédiction

En savoir plus

Références

[1] S. K. Zhou, H. Greenspan, C. Davatzikos, J. S. Duncan, B. van Ginneken, A. Madabhushi, J. L.Prince, D. Rueckert, and R. M. Summers, “A review of deep learning in medical imaging : Imagingtraits, technology trends, case studies with progress highlights, and future promises,”Proceedingsof the IEEE, 2021.

[2] J. R. Zech, M. A. Badgeley, M. Liu, A. B. Costa, J. J. Titano, and E. K. Oermann, “Confoundingvariables can degrade generalization performance of radiological deep learning models,”arXivpreprint arXiv :1807.00431, 2018.

[3] S. Lapuschkin, S. Wäldchen, A. Binder, G. Montavon, W. Samek, and K.-R. Müller, “Unmaskingclever hans predictors and assessing what machines really learn,”Nature communications, vol. 10,no. 1, pp. 1–8, 2019.

[4]"Rétinopathiediabétique-snof.”https://www.snof.org/encyclopedie/r%C3%A9tinopathie-diab%C3%A9tique. Accessed : 2020.

[5] “Eye-quality (eyeq) assessment dataset.”https://github.com/HzFu/EyeQ. Accessed : 2019.

[6] H. Fu, B. Wang, J. Shen, S. Cui, Y. Xu, J. Liu, and L. Shao, “Evaluation of retinal image qualityassessment networks in different color-spaces,” inInternational Conference on Medical ImageComputing and Computer-Assisted Intervention, pp. 48–56, Springer, 2019.

[7] M. Poceviči ̄ut ̇e, G. Eilertsen, and C. Lundström, “Survey of xai in digital pathology,” inArtificialIntelligence and Machine Learning for Digital Pathology, pp. 56–88, Springer, 2020.

[8] D. T. Huff, A. J. Weisman, and R. Jeraj, “Interpretation and visualization techniques for deeplearning models in medical imaging,”Physics in Medicine & Biology, vol. 66, no. 4, p. 04TR01,2021.

[9] B. Zhou, A. Khosla, A. Lapedriza, A. Oliva, and A. Torralba, “Learning deep features for dis-criminative localization,” inProceedings of the IEEE conference on computer vision and patternrecognition, pp. 2921–2929, 2016.

[10] R. R. Selvaraju, M. Cogswell, A. Das, R. Vedantam, D. Parikh, and D. Batra, “Grad-cam :Visual explanations from deep networks via gradient-based localization,” inProceedings of theIEEE international conference on computer vision, pp. 618–626, 2017.

[11] A. Chattopadhay, A. Sarkar, P. Howlader, and V. N. Balasubramanian, “Grad-cam++ : Genera-lized gradient-based visual explanations for deep convolutional networks,” in2018 IEEE WinterConference on Applications of Computer Vision (WACV), pp. 839–847, IEEE, 2018.

[12] K. Simonyan, A. Vedaldi, and A. Zisserman, “Deep inside convolutional networks : Visualisingimage classification models and saliency maps,”arXiv preprint arXiv :1312.6034, 2013.

[13] D. Smilkov, N. Thorat, B. Kim, F. Viégas, and M. Wattenberg, “Smoothgrad : removing noiseby adding noise,”arXiv preprint arXiv :1706.03825, 2017.

[14] M. T. Ribeiro, S. Singh, and C. Guestrin, “" why should i trust you ?" explaining the predictions ofany classifier,” inProceedings of the 22nd ACM SIGKDD international conference on knowledgediscovery and data mining, pp. 1135–1144, 2016.

[15] “Comparison of segmentation and superpixel algorithms - scikit-image.”https://scikit-image.org/docs/stable/auto_examples/segmentation/plot_segmentations.html.Accessed :2020.

[16] M. Alam, Y. Zhang, J. I. Lim, R. Chan, M. Yang, and X. Yao, “Quantitative oct angiographyfeatures for objective classification and staging of diabetic retinopathy,”Retina (Philadelphia,Pa.).